[转] Quake-III 代码里神奇的浮点开方函数

prog
留言

源贴在这里 (也是转帖): http://www.douban.com/note/196653073/

Quake-III 代码里神奇的浮点开方函数

Quake-III Arena (雷神之锤3) 是90年代的经典游戏之一. 该系列的游戏不但画面和内容不错, 而且即使计算机配置低, 也能极其流畅地运行. 这要归功于它3D引擎的开发者约翰-卡马克(John Carmack).

事实上早在90年代初DOS时代, 只要能在PC上搞个小动画都能让人惊叹一番的时候, John Carmack 就推出了石破天惊的Castle Wolfstein, 然后再接再励, doom, doomII, Quake…每次都把 3-D 技术推到极致. 他的3D引擎代码极度高效, 几乎是在压榨PC机的每条运算指令. 当初MS的 Direct3D 也得听取他的意见, 修改了不少API.

最近, QUAKE的开发商 ID SOFTWARE 遵守GPL协议, 公开了QUAKE-III的原代码, 让世人有幸目睹Carmack传奇的3D引擎的原码. 这是QUAKE-III原代码的下载地址:
http://www.fileshack.com/file.x?fid=7547

(下面是官方的下载网址, 搜索 quake3-1.32b-source.zip 可以找到一大堆中文网页的
ftp://ftp.idsoftware.com/idstuff/source/quake3-1.32b-source.zip)

我们知道, 越底层的函数, 调用越频繁. 3D引擎归根到底还是数学运算. 那么找到最底层的数学运算函数 (在 game/code/q_math.c), 必然是精心编写的. 里面有很多有趣的函数, 很多都令人惊奇, 估计我们几年时间都学不完.

在 game/code/q_math.c 里发现了这样一段代码. 它的作用是将一个数开平方并取倒, 经测试这段代码比 (float)(1.0/sqrt(x)) 快4倍:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threehalfs = 1.5F;

    x2 = number * 0.5F;
    y   = number;
    i   = * ( long * ) &y;   // evil floating point bit level hacking
    i   = 0x5f3759df - ( i >> 1 ); // what the fuck?
    y   = * ( float * ) &i;
    y   = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
    // y   = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed

    #ifndef Q3_VM
    #ifdef __linux__
     assert( !isnan(y) ); // bk010122 - FPE?
    #endif
    #endif
    return y;
}

函数返回 1/sqrt(x), 这个函数在图像处理中比 sqrt(x) 更有用. 注意到这个函数只用了一次叠代! (其实就是根本没用叠代, 直接运算). 编译, 实验, 这个函数不仅工作的很好, 而且比标准的 sqrt() 函数快4倍! 要知道, 编译器自带的函数, 可是经过严格仔细的汇编优化的啊!

这个简洁的函数, 最核心, 也是最让人费解的, 就是标注了 what the fuck? 的一句
i = 0x5f3759df - ( i >> 1 ); 再加上 y = y * ( threehalfs - ( x2 * y * y ) ); 两句话就完成了开方运算! 而且注意到, 核心那句是定点移位运算, 速度极快! 特别在很多没有乘法指令的RISC结构CPU上, 这样做是极其高效的.

算法的原理其实不复杂, 就是牛顿迭代法, 用 x-f(x)/f'(x) 来不断的逼近 f(x)=a的根.

简单来说比如求平方根, f(x)=x^2=a, f'(x)= 2*x, f(x)/f'(x)=x/2, 把f(x)代入
x-f(x)/f'(x) 后有 (x+a/x)/2, 现在我们选 a=5, 选一个猜测值比如2, 那么我们可以这么算 5/2 = 2.5; (2.5+2)/2 = 2.25; 5/2.25 = xxx; (2.25+xxx)/2 = xxxx ... 这样反复迭代下去, 结果必定收敛于 sqrt(5).

没错, 一般的求平方根都是这么算的. 但是卡马克(quake3作者)真正牛B的地方是他选择了一个神秘的常数 0x5f3759df 来计算那个猜测值. 就是我们加注释的那一行, 那一行算出的值非常接近 1/sqrt(n),这样我们只需要2次牛顿迭代就可以达到我们所需要的精度.

好吧, 如果这个还不算NB, 接着看:

普渡大学的数学家Chris Lomont看了以后觉得有趣, 决定要研究一下卡马克弄出来的
这个猜测值有什么奥秘. Lomont也是个牛人, 在精心研究之后从理论上也推导出一个
最佳猜测值, 和卡马克的数字非常接近, 0x5f37642f. 卡马克真牛, 他是外星人吗？

传奇并没有在这里结束. Lomont计算出结果以后非常满意, 于是拿自己计算出的起始
值和卡马克的神秘数字做比赛, 看看谁的数字能够更快更精确的求得平方根. 结果是
卡马克赢了… 谁也不知道卡马克是怎么找到这个数字的.

最后 Lomont怒了, 采用暴力方法一个数字一个数字试过来, 终于找到一个比卡马克数
字要好上那么一丁点的数字, 虽然实际上这两个数字所产生的结果非常近似, 这个暴
力得出的数字是 0x5f375a86.

Lomont为此写下一篇论文, "Fast Inverse Square Root".

论文下载地址:

http://www.math.purdue.edu/~clomont/Math/Papers/2003/InvSqrt.pdf
http://www.matrix67.com/data/InvSqrt.pdf

参考: <IEEE Standard 754 for Binary Floating-Point Arithmetic><FAST INVERSE SQUARE ROOT>

最后, 给出最精简的 1/sqrt() 函数:

1
2
3
4
5
6
7
8
9
float InvSqrt(float x)
{
    float xhalf = 0.5f*x;
    int i = *(int*)&x; // get bits for floating VALUE
    i = 0x5f375a86- (i>>1); // gives initial guess y0
    x = *(float*)&i; // convert bits BACK to float
    x = x*(1.5f-xhalf*x*x); // Newton step, repeating increases accuracy
    return x;
}

大家可以尝试在PC机、51、AVR、430、ARM、上面编译并实验, 惊讶一下它的工作效率.

前兩天有一則新聞, 大意是說 Ryszard Sommefeldt 很久以前看到這麼樣的一段 code (可能出自 Quake III 的 source code):

1
2
3
4
5
6
7
8
9
float InvSqrt (float x) {
    float xhalf = 0.5f*x;
    int i = *(int*)&x;
    i = 0x5f3759df - (i>>1);
    x = *(float*)&i;
    x = x*(1.5f - xhalf*x*x);
    return x;

}

他一看之下驚為天人, 想要拜見這位前輩高人, 但是一路追尋下去卻一直找不到人; 同時間也有其他人在找, 雖然也沒找到出處, 但是 Chris Lomont 寫了一篇論文 (in PDF) 解析這段 code 的演算法 (用的是 Newton’s Method, 牛頓法; 比較重要的是後半段講到怎麼找出神奇的 0x5f3759df 的).

PS. 這個 function 之所以重要, 是因為求 開根號倒數 這個動作在 3D 運算 (向量運算的部份) 裡面常常會用到, 如果你用最原始的 sqrt() 然後再倒數的話, 速度比上面的這個版本大概慢了四倍吧… XD

PS2. 在他們追尋的過程中, 有人提到一份叫做 MIT HACKMEM 的文件, 這是 1970 年代的 MIT 強者們做的一些筆記 (hack memo), 大部份是 algorithm, 有些 code 是 PDP-10 asm 寫的, 另外有少數是 C code (有人整理了一份列表).

附: 牛顿迭代法快速寻找平方根

下面这种方法可以很有效地求出根号a的近似值: 首先随便猜一个近似值x, 然后不断令x等于 x 和 a/x 的平均数, 迭代个六七次后 x 的值就已经相当精确了. 例如, 我想求根号 2 等于多少. 假如我猜测的结果为4, 虽然错的离谱, 但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了:

1
2
3
4
5
(       4   + 2/   4     ) / 2 = 2.25
(     2.25   + 2/   2.25   ) / 2 = 1.56944..
( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
( 1.42189..+ 2/1.42189..) / 2 = 1.41423..
....

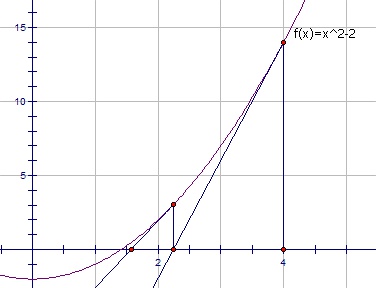
这种算法的原理很简单, 我们仅仅是不断用 (x, f(x)) 的切线来逼近方程 x^2-a=0的根. 根号a实际上就是 x^2-a=0的一个正实根, 这个函数的导数是2x. 也就是说, 函数上任一点 (x,f(x))处的切线斜率是2x. 那么, x-f(x)/(2x) 就是一个比 x 更接近的近似值. 代入 f(x)=x^2-a 得到 x-(x^2-a)/(2x), 也就是 (x+a/x)/2.